El movimiento de los espermatozoides sigue el mismo patrón que la configuración de las rayas de las cebras

Publicado originalmente por la Universidad de Bristol el 27 de septiembre de 2023

 

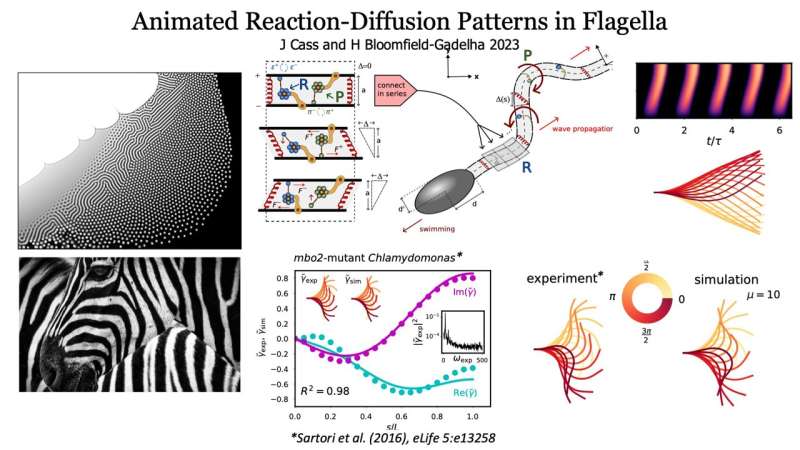
Gráfico. Crédito: Hermes Gadêlha

Se cree que los patrones de interacciones químicas crean patrones en la naturaleza como las rayas y las manchas. Un nuevo estudio demuestra que la base matemática de estos patrones también rige el movimiento de la cola de los espermatozoides.

Los hallazgos, publicados el 27 de septiembre de 2023, en Nature Communications, revelan que el movimiento flagelar de, por ejemplo, las colas de los espermatozoides y los cilios, sigue la misma pauta de formación de patrones que descubrió el matemático Alan Turing.

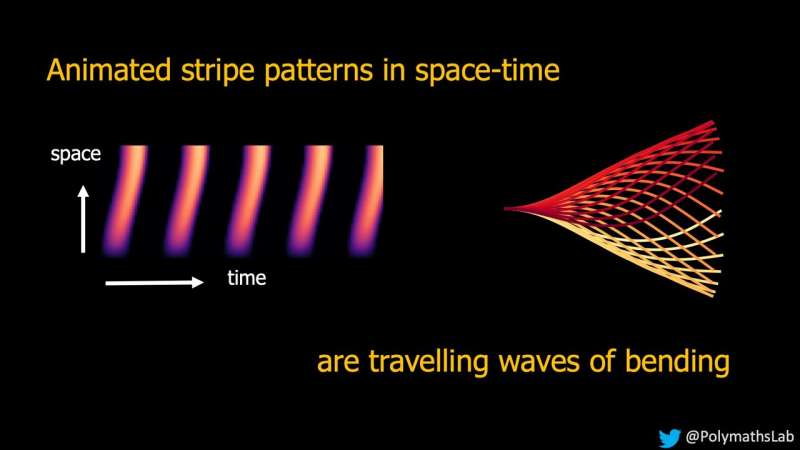
Las ondulaciones de los flagelos crean patrones de movimiento en el espacio-tiempo, generando ondas que viajan a lo largo de la cola para impulsar el avance de los espermatozoides y los microbios.

Alan Turing es conocido sobre todo por ayudar a descifrar el código enigma durante la Segunda Guerra Mundial. Sin embargo, también desarrolló una teoría de la formación de patrones que predecía que los patrones químicos pueden aparecer espontáneamente con sólo dos ingredientes: sustancias químicas que se difunden y que reaccionan entre sí. Turing propuso por primera vez la llamada teoría de la reacción-difusión para la formación de patrones.

Turing ayudó a allanar el camino a un nuevo tipo de investigación que utiliza las matemáticas de la reacción-difusión para comprender los patrones naturales. Hoy en día, estos patrones químicos imaginados por Turing se denominan patrones de Turing. Aunque aún no se ha demostrado experimentalmente, se cree que estos patrones rigen muchos patrones de la naturaleza, como las manchas de los leopardos, el verticilo de semillas en la cabeza de un girasol y los patrones de la arena en la playa. La teoría de Turing puede aplicarse a diversos campos, desde la biología y la robótica hasta la astrofísica.

Vídeo explicativo. Crédito: Hermes Gadêlha

El matemático Hermes Gadêlha, director del Laboratorio de Polímeros de la Universidad de Bristol, y su estudiante de doctorado James Cass llevaron a cabo esta investigación en la Escuela de Ingeniería Matemática y Tecnología de la Universidad de Bristol.

Gadêlha explica: "El movimiento espontáneo de los flagelos y cilios se observa en todas partes en la naturaleza, pero se sabe poco sobre cómo se orquesta. Es fundamental en la salud y la enfermedad, la reproducción, la evolución y la supervivencia de casi todos los microorganismos de la Tierra que se desplazan en un medio acuático".

El equipo se inspiró en observaciones recientes de fluidos de baja viscosidad según las cuales el entorno desempeña un papel menor en el flagelo. Utilizaron modelos matemáticos, simulaciones y técnicas de ajuste de datos para demostrar que las ondulaciones de los flagelos pueden surgir espontáneamente sin que influya el entorno fluido en el que se mueven.

Matemáticamente, esto equivale al sistema de reacción-difusión de Turing, que se propuso por primera vez para los patrones químicos.

Patrones de rayas. Crédito: Hermes Gadêlha

En el caso de la natación de los espermatozoides, las reacciones químicas de los motores moleculares impulsan el flagelo, y el movimiento de flexión se difunde a lo largo de la cola en forma de ondas. El nivel de similitud entre los patrones visuales y los patrones de movimiento es sorprendente e inesperado y demuestra que sólo se necesitan dos ingredientes simples para lograr un movimiento altamente complejo.

El Dr. Gadêlha añadió: "Demostramos que esta 'receta' matemática la siguen dos especies muy distantes: el espermatozoide del toro y las Chlamydomonas (un alga verde que se utiliza como organismo modelo en toda la ciencia), lo que sugiere que la naturaleza reproduce soluciones similares". Las ondas viajeras surgen espontáneamente incluso cuando el flagelo no se ve influido por el fluido circundante. Esto significa que el flagelo dispone de un mecanismo infalible para permitir la natación en entornos de baja viscosidad, lo que de otro modo sería imposible para las especies acuáticas.

"Es la primera vez que las simulaciones de modelos encajan con los datos experimentales. Estamos muy agradecidos a los investigadores que pusieron sus datos a libre disposición, sin los cuales no habríamos podido seguir adelante con este estudio matemático."

Patrones de rayas en el espacio-tiempo. Crédito: Hermes Gadêlha

Estos hallazgos podrían utilizarse en el futuro para comprender mejor los problemas de fertilidad asociados al movimiento flagelar anormal y otras ciliopatías; enfermedades causadas por la ineficacia de los cilios en los humanos.

También podría tener aplicaciones robóticas, para músculos artificiales y materiales animados, ya que el equipo ha descubierto una sencilla "receta matemática" para crear patrones de movimiento.

El Dr. Gadêlha también es miembro del Laboratorio SoftLab de Robótica de Bristol (BRL), donde utiliza las matemáticas de formación de patrones para innovar en la próxima generación de robots blandos.

"En 1952, Turing desveló la base de reacción-difusión de los patrones químicos", explica Gadêlha. "Demostramos que el 'átomo' del movimiento en el mundo celular, el flagelo, utiliza la plantilla de Turing para dar forma a patrones de movimiento que impulsan el movimiento de la cola y que empuja a los espermatozoides hacia delante".

"Aunque esto supone un paso más hacia la descodificación matemática de la animación espontánea en la naturaleza, nuestro modelo de reacción-difusión es demasiado simple para captar plenamente toda su complejidad. Es posible que existan otros modelos, que se ajusten a los experimentos igual o incluso mejor, de cuya existencia simplemente aún no tenemos conocimiento y, por tanto, es necesario seguir investigando".

El trabajo numérico se llevó a cabo utilizando las instalaciones de cálculo y almacenamiento de datos del Centro de Investigación Informática Avanzada de la Universidad de Bristol.

Para más información: The reaction-diffusion basis of animated patterns in eukaryotic flagella, Nature Communications (2023). DOI: 10.1038/s41467-023-40338-2 , https://www.nature.com/articles/s41467-023-40338-2

Información de la revista: Nature Communications

Proporcionado por la Universidad de Bristol.